Talk:Gnaiger 2020 MitoFit x
From Bioblast
Canonical reviewer's comments on: Bureau International des Poids et Mesures (2019) The International System of Units (SI) 9th ed.
Communicated by Gnaiger Erich (2020-07-05) last update 2020-08-11 in: Anastrophe XX Entity X and elementary unit x of A X-mass Carol
Summary
- The 9th edition of ‘The International System of Units (SI)’ released on 2019-May-20 introduced a new approach by defining the SI base units — and thus the abstract SI units in general — by their relation to fixed numerical values of fundamental constants of nature. Previous definitions of abstract units relied on a reference to concrete individual things realized as material artefacts, such as the International Prototype of the Kilogram (IPK). The (general) abstract unit ‘kilogram’ had to be calibrated in balance against an (individual) ‘entetic’ unit defining “1 kg” as a reference. This defined not only the unit of mass but also the mole [mol] as the unit of amount. Now the SI defines the mole as the fixed number of entities given by the Avogadro constant NA. The elementary charge e is a fixed number of charges per proton. Amount and charge are thus in a fixed relation to the count of elementary entities UX [x]. Count, amount, and charge are isomorphic elementary quantities. Amount and charge are linked to the count NX = N∙UX with elementary unit x by fixed conversion constants NA-1 [mol∙x−1] and e [C∙x−1], respectively. The SI does not use the elementary unit x. This causes a number of formal inconsistencies as discussed in the present communication.
Introduction

"The former International Prototype of the Kilogram (IPK) is an artefact whose mass defined the SI unit of mass until the implementation of a revised definition of the kilogram on 20 May 2019. .. The unit of mass is disseminated throughout the world by comparisons with the IPK made indirectly through a hierarchical system of mass standards. Historically the IPK has been compared to its official copies at intervals of about 40 years, with the exception of the "extraordinary campaign" carried out in 2014, which was only 22 years after the preceding one. In the intervals in between, the working standards are used to disseminate the kilogram unit to the Member States by calibrations of their "national prototypes", which are intended to serve as national standards." — https://www.bipm.org/en/bipm/mass/ipk/
- Thinking quantitatively is not easy outside very simply perceived and commonly encountered instances in every-day life. The number of individual persons in a family or individual collaborators in a company is a count, expressed by most societies and in most (but not all) languages in the same abstract unit that is understood intuitively and does not need an international convention. In contrast, the mass of the earth is beyond our perception, and the mass of the International Prototype of the Kilogram (IPK) may appear as abstract as the unit kilogram itself, despite the fact that the IPK is a real artefact, a single individual thing, which is Euclid's definition of the unit. The International System of Units takes care of abstract units, which have their roots in real, material units, which are the defining realizations as artefacts or prototypes of a unit, such as the IPK. Some abstract units are far removed from our perception, such as the joule. There are scientists, who think of units of temperature in terms Celsius [°C] in the lab, but Fahrenheit [°F] at home. Several scientific journals recommend to report data in SI units, but in the same journals we find respiration reported in time units of minutes [min], energy in units of calories [cal], and respiration as volume instead of molar amount of oxygen. This disconnects us from grasping quantitative terms — or do you have a quick recognition of the meaning 168.3 dozens of years? In 2020 we still cannot convince authors and journals to consistently use SI units.
- One area where a problem is encountered in the International System of Units is the quantity 'count'. This accounts for substantial difficulties in general. How consistent are we in the formal use of the basic terms 'count' and 'number'? Can we refer to quickly recognizable disambiguous terms for quantities normalized for a count, such as mass, volume, or rate per count? In a position statement on quantitative 'Mitochondrial physiology', it was difficult to follow SI guidelines on units of the quantity 'count', and in distinguishing the mass or volume of cells or organisms, versus mass or volume per single individual cell or organism (Gnaiger et al 2020). Whereas ad-hoc terms and symbols may be easily invented in a single publication or in practical language during a lecture, it is not easy to predict, if such invented terms are actually understood or properly decoded. Since even statisticians are quickly ready to present an apparently coherent story in view of few data (Kahneman 2011), I predict that misunderstandings of normalizations per count are the norm in some areas of the biomedical literature. Most importantly, in a general position statement, ad-hoc invented terms and symbols cannot be tolerated, but a consistent and coherent nomenclature is required with proper definitions. The difficulties may appear to be trivial, since counting and the unit linked to counting is not expected to present any significant problems. Counting is such a basic, fundamental, simple thing, deeply implemented in our common language. Did you realize the following terms used in this paragraph above: count, encounter, account? The fictitious 'Canonical reviewer's comments' on the probably most fundamental and formal publication in the scientific literature provides a better feeling than a theoretical treatise for a scientific readership to realize the actual problems and potential solutions offered in the publication BEC 2020.1. For the meaning of the term ‘canonical’ I refer to Hofstadter (1979). For the practical side of canonical pages, use numerical and canonical pages on opposite sides.
Canonical reviewer's general comments
- This SI publication is one of the most significant scientific, interdisciplinary and transdisciplinary publications of the century. Too many teachers and editors resist to making it a highly influential publication with actual impact on scientific publication, and thus contribute to the current communication crisis. This does not reflect any faults of the SI authors but a lack of governance to improve scientific communication, and the limitations of the non-SI readers trapped into the International System of Impact Factors rather than guided towards implementing the International System of Units. What is the numerical value and the practical meaning of the Impact Factor of this SI publication?
- Quantity values being pure numbers (Section 5.4.7 Stating quantity values being pure numbers; p. 151):
- "As discussed in Section 2.3.3, values of quantities with unit one, are expressed simply as numbers. The unit symbol 1 or unit name “one” are not explicitly shown. SI prefix symbols can neither be attached to the symbol 1 nor to the name “one”, therefore powers of 10 are used to express particularly large or small values."
- What are — apart from ratios of quantities — these "quantities with unit one"?
- Quantity values being pure numbers (Section 5.4.7 Stating quantity values being pure numbers; p. 151):
The quantity count
- Section 2.3.3 Dimensions of quantities: On p. 136, the quantity count is mentioned:
- "All other quantities, with the exception of counts, are derived quantities, which may be written in terms of base quantities according to the equations of physics. .. There are also some quantities that cannot be described in terms of the seven base quantities of the SI, but have the nature of a count. Examples are a number of molecules, a number of cellular or biomolecular entities (for example copies of a particular nucleic acid sequence), or degeneracy in quantum mechanics. Counting quantities are also quantities with the associated unit one."
- Importantly and surprisingly, a general definition of the quantity count is missing. This is particularly disconcerting, since it appears to ignore the specific emphasis placed on clarification on p. 137:
- "It is especially important to have a clear description of any quantity with unit one (see section 5.4.7) that is expressed as a ratio of quantities of the same kind (for example length ratios or amount fractions) or as a count (for example number of photons or decays)."
- In section 5.4.7 (p. 151): "Quantities relating to counting do not have this option {of being expressed with units (m/m, mol/mol)}, they are just numbers."
- On p. 140: "the SI unit of activity is becquerel, implying counts per second".
- These phrases are the only places where count(s) and counting are mentioned in the SI document, besides 'counting fringes' (p. 207: ".. using an interferometer with a travelling microscope to measure the optical path difference as the fringes were counted") and p. 129.
- Section 2.3.3 Dimensions of quantities: On p. 136, the quantity count is mentioned:
Unit of count
- On p. 129 a "quantity for counting entities" is given as NA times amount of substance.
- "The Avogadro constant NA is a proportionality constant between the quantity amount of substance (with unit mole) and the quantity for counting entities (with unit one, symbol 1)."
- A unit should not be a number, and the symbol for a unit should not be a numeral. In Resolution 1 (p. 189) a consensus is reached on the importance of "a redefinition of a number of units of the International System of Units (SI)".
- On p. 129 a "quantity for counting entities" is given as NA times amount of substance.
- The definition of count and redefinition of the unit of count remain an open task.
Technical comments
Spelling
- Since 'small spelling variations occur in the language of the English speaking countries (for instance, "metre" and "meter", "litre" and "liter")' (p. 124), a decision should be taken for consistent spelling in a document. The English text of the SI brochure follows the style "metre" and "litre". It is found that in the scientific literature the spelling style "meter" and "liter" prevails even in European journals. In the following quotes from the SI brochure (with reference to page numbers in the 9th edition), the spelling style is changed, which does not exert any influence on the meaning.
Quantity calculus (p. 148)
- "Symbols for units are treated as mathematical entities. In expressing the value of a quantity as the product of a numerical value and a unit, both the numerical value and the unit may be treated by the ordinary rules of algebra. This procedure is described as the use of quantity calculus, or the algebra of quantities. For example, the equation p = 48 kPa may equally be written as p/kPa = 48. It is common practice to write the quotient of a quantity and a unit in this way for a column heading in a table, so that the entries in the table are simply numbers."
Suggestion: pO2/[kPa] = 18.6; SO2/[µmol·kPa-1] = 9.72 Without changing any of the above rules, it is useful to put units into brackets to designate the units specifically in quantity calculus.
No comment
Defining the unit of a quantity (p. 127)
- "The value of a quantity is generally expressed as the product of a number and a unit. The unit is simply a particular example of the quantity concerned which is used as a reference, and the number is the ratio of the value of the quantity to the unit.
- "For example, the speed of light in vacuum is a constant of nature, denoted by c, whose value in SI units is given by the relation c = 299 792 458 m/s where the numerical value is 299 792 458 and the unit is m/s.
- "For a particular quantity different units may be used. For example, the value of the speed v of a particle may be expressed as v = 25 m/s or v = 90 km/h, where meter per second and kilometer per hour are alternative units for the same value of the quantity speed.
- "Before stating the result of a measurement, it is essential that the quantity being presented is adequately described. This may be simple, as in the case of the length of a particular steel rod, but can become more complex when higher accuracy is required and where additional parameters, such as temperature, need to be specified.
- "When a measurement result of a quantity is reported, the estimated value of the measurand (the quantity to be measured), and the uncertainty associated with that value, are necessary. Both are expressed in the same unit."
Canonical comments
Definition of the SI (p. 127)
- "As for any quantity, the value of a fundamental constant can be expressed as the product of a number and a unit."
- "The definitions below specify the exact numerical value of each constant when its value is expressed in the corresponding SI unit. By fixing the exact numerical value the unit becomes defined, since the product of the numerical value and the unit has to equal the value of the constant, which is postulated to be invariant."
Comment: The terms 'number' and 'numerical value' are used as being equivalent in the two phrases above: (1) value of a fundamental constant = "product of a number and a unit"; (2) value of the constant = "product of the numerical value and the unit".
It should be considered to define: The value of a quantity Q (QX or Qu) is the product of the numerical value of a number N and a unit u. Symbols for quantities QX are, e.g., NX and nX for count and amount, respectively; symbols for quantities Qu are, e.g., m and V for mass and volume, respectively. Do these symbols represent merely the quantity type? Interpret a formula such as m = 60 kg: The symbol m represents the quantity 'mass', the numerical value of the number N is 60 (N = 60), the unit is um = kg, and the value of the quantity m is 60 kg. Just in case that these definitions appear to be acceptable, then it follows: quantity m = value of the quantity m. The number N is not a quantity, since it has no units, and the numerical value of a number N is a pure number. N is the symbol for any number, and 60 is the numeral for the number with numerical value of 60 = 6·10.
- "The seven constants are chosen in such a way that any unit of the SI can be written either through a defining constant itself or through products or quotients of defining constants.
- The International System of Units, the SI, is the system of units in which
- the unperturbed ground state hyperfine transition frequency of the caesium 133 atom ∆νCs is 9 192 631 770 Hz,
- the speed of light in vacuum c is 299 792 458 m/s,
- the Planck constant h is 6.626 070 15 × 10−34 J s,
- the elementary charge e is 1.602 176 634 × 10−19 C x-1,
- the Boltzmann constant k is 1.380 649 × 10−23 J x-1 K-1,
- the Avogadro constant NA is 6.022 140 76 × 1023 x mol−1,
- the luminous efficacy of monochromatic radiation of frequency 540 × 1012 Hz, Kcd, is 683 lm/W,
- where the hertz, joule, coulomb, lumen, and watt, with unit symbols Hz, J, C, lm, and W, respectively, are related to the units second, meter, kilogram, ampere, kelvin, mole, and candela, with unit symbols s, m, kg, A, K, mol, and cd, respectively, according to Hz = s–1, J = kg m2 s–2, C = A s, lm = cd m2 m–2 = cd sr, and W = kg m2 s–3.
- The numerical values of the seven defining constants have no uncertainty."
The nature of the seven defining constants (p. 129)
- "The Avogadro constant NA is a proportionality constant between the quantity amount of substance (with unit mole) and the quantity for counting entities (with unit one, symbol 1)."
Comment: Comparing the terms 'quantity amount of substance (with unit mole)' and 'quantity for counting entities (with unit one, symbol 1)' raises several questions that lead to the following comments:
(1) For 'quantity for counting entities' the proper name should be given, comparable to amount. A proper name is count.
(2) The term 'quantity for counting entities' is ambiguous: Is it a quantity for counting? Is it a quantity for entities that are counting (entities such as counting machines, cell counters, ticket counters)?
(3) Unit one, symbol 1: This is a profound mixup of a numerical value or number 'one' (numeral 1) with a unit. There is an inconsistency compared to all other units in the SI, since the 'one' (numeral 1) could be added to any other SI unit, e.g. volume per mass V/m with unit [m3]/[1 kg] instead of [m3]/[kg], compared to volume per count V/NX with unit [m3]/[1 x] instead of [m3]/[x].
Quantity symbols and unit symbols (p. 149)
- "Unit symbols must not be used to provide specific information about the quantity and should never be the sole source of information on the quantity. Units are never qualified by further information about the nature of the quantity; any extra information on the nature of the quantity should be attached to the quantity symbol and not to the unit symbol."
Comment: "Units are never qualified by further information about the nature of the quantity" — this generalization is valid only for units restricted to the class of abstract units u. Units u are abstracted from the nature of the entity X which is expressed as a quantity Qu. In contrast, it is essential to qualify any Euclidean unit UX by X as the defining 'single individual thing': the unit particle, the unit atom O, the unit O2 molecule, the unit endothelial cell, the unit organism of type org, the unit event of type X.
The term "nature of the quantity" is ambiguous, with potentially dualistic meaning as (1) the nature of the quantity being mass, length, volume, amount of substance, etc.; or (2) the nature of entity X of the quantity, meaning a volume of O2 versus CO2, a mass of pudding or stones, etc. Did SI intend the second interpretation, or both?
Quantity calculus can be complemented by providing specific information about the entity (e.g. entity O2) separate from the unit symbol (not attached to the unit symbol), but subsequent to the unit symbol, e.g., [mol O2] or [kJ·mol-1 O2], such that the entity-type is not presented in the place occupied by the unit symbol for division or multiplication, respectively.
Writing and printing of unit symbols and of numbers — Resolution 7 (p. 162)
- "Roman (upright) type, in general lower-case, is used for symbols of units; if, however, the symbols are derived from proper names, capital roman type is used. These symbols are not followed by a full stop."
Comment: The SI symbol '1' suggested for the unit of the quantity count, does not follow this SI procedure. A symbol for the unit of count is required, that is consistent with SI Resolution 7.
- "In numbers, the comma (French practice) or the dot (British practice) is used only to separate the integral part of numbers from the decimal part. Numbers may be divided in groups of three in order to facilitate reading; neither dots nor commas are ever inserted in the spaces between groups."
Comment: In the last sentence above, there is a confusion between numbers, numerals (representing numbers, such as 4, 12, 5093.78, 6, in a specific numeral system), and digits (or characters, such as the ten characters in the decimal numeral system: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ). When a large number is expressed by a numeral as a string of several symbols, the digits may be separated in groups of three ..
For comparison, IUPAC presents the same message in the following correct form: "To facilitate the reading of long numbers the digits may be grouped in threes about the decimal sign but no point or comma should be used except for the decimal sign."
The historical development of the realization of SI units (p. 204)
- ".. the masses of a silicon atom (averaged over the three isotopes used for the sphere) mSi, and the electron me .."
Comment: Defining entity X as Si, the SI symbol for the mass of a sample of Si is mSi. From a count NSi of Si in the sample, the mass per silicon atom is mSi·NSi-1. The same holds for the mass per any elementary entity of entity-type X. For consistency, the general term 'mass of an entity' ("masses of a silicon atom .. and the electron") has to be replaced by the general term 'mass per elementary entity' as proposed by Gnaiger et al 2020 ("masses per silicon atom .. and per electron"). The symbol mSi cannot be used for the expression mSi·NSi-1. This elementary, formal inconsistency must be resolved in the SI to achieve coherence. Elementary mass per Si atom is MUSi = mSi·(N·USi)-1.
Unit of amount of substance, mole (p. 209)
- "The quantity used by chemists to specify the amount of chemical elements or compounds is called “amount of substance”. Amount of substance, symbol n, is defined to be proportional to the number of specified elementary entities N in a sample, the proportionality constant being a universal constant which is the same for all entities. The proportionality constant is the reciprocal of the Avogadro constant NA, so that n = N/NA. The unit of amount of substance is called the mole, symbol mol. Following proposals by the IUPAP, IUPAC and ISO, the CIPM developed a definition of the mole in 1967 and confirmed it in 1969, by specifying that the molar mass of carbon 12 should be exactly 0.012 kg/mol. This allowed the amount of substance nS(X) of any pure sample S of entity X to be determined directly from the mass of the sample mS and the molar mass M(X) of entity X, the molar mass being determined from its relative atomic mass Ar (atomic or molecular weight) without the need for a precise knowledge of the Avogadro constant, by using the relations
nS(X) = mS/M(X), and M(X) = Ar(X) g/mol
- Thus, this definition of the mole was dependent on the artefact definition of the kilogram. The numerical value of the Avogadro constant defined in this way was equal to the number of atoms in 12 grams of carbon 12. However, because of recent technological advances, this number is now known with such precision that a simpler and more universal definition of the mole has become possible, namely, by specifying exactly the number of entities in one mole of any substance, thus fixing the numerical value of the Avogadro constant. This has the effect that the new definition of the mole and the value of the Avogadro constant are no longer dependent on the definition of the kilogram."
Comment (1): Clarification is required to explain the difference between a number and a "number of specified elementary entities N in a sample". If symbol N is used to represent a 'number of specified elementary entities', then the same symbol N cannot be used to represent a 'number'. The term 'number' is used in defining the unit of a quantity (Section 2.1): "The value of a quantity is generally expressed as the product of a number and a unit." Distinguishable symbols should be used for "number of entities" NX with elementary unit [x] and dimensionless "number" N (without subscript; Gnaiger et al 2020). It might be appropriate, to use the lower case n for dimensionless number, but this is not practical, since it might be confused with the symbol n for amount, as in nX = NX/NA.
Comment (2): The terms entity and entities are used with two different meanings. Whereas these meanings can be more or less perfectly understood by decoding in context using practical language, this ambiguity should be avoided in a formal system of terminology: (i) In the context "amount of substance nS(X) of any pure sample S of entity X", and "molar mass M(X) of entity X", the term entity and symbol X are used with the meaning entity-type. (ii) If this interpretation in terms of specification of entity-type is taken rigorously, then the term "by specifying exactly the number of entities in one mole of any substance, thus fixing the numerical value of the Avogadro constant" must be understood as indicating, that in one mole of any such substance there are NA different entity-types. The intention of this comment is not to suggest, that anybody should make such a non-sensical interpretation, but rather to point to the formal inconsistency of the terminological system. The SI lacks a distinction between the term entity-type X (which does not express any quantity) and the elementary entity UX (which is an 'external' elementary quantity that needs to be defined before counting can start with a count NX = 1 x). With this clarification in mind, it then makes sense to use practical language: (i) "sample S of entity X"; (ii) "number of elementary entities" = count, NX = N·UX with elementary unit [x] (Gnaiger et al 2020).
Comment (3): The symbols nS(X) and mS are well defined, such that the meaning of the message can be understood. There remains, however, the difficulty to understand the logic of selecting these symbols. The amount nS(X) [mol] of X can be calculated from the mass mS [g] of pure sample S and the molar mass M(X) [g·mol-1] of entity X only, if there is a pure sample S of entity X. Why then is this essential information not added to the symbol mS(X), comparable to nS(X)?
Comment (4): If mS or mS(X) [g] is the symbol for the mass of a pure sample of entity X, and nS(X) [mol] is the symbol for amount of substance of a pure sample S of entity X, are these then equivalent to mX [g] and nX [mol], respectively, as the symbols for the mass and amount of entity X? Can a mass or amount be determined for an entity X that is not sampled? It may be clarified, that a quantity by definition can be measured (mass) or counted (amount) only in a defined sample of a defined entity X. It should be noted that "defined entity X" may be something rather undefined: A number of trees can be sampled; the mass of these trees can be measured; the number of trees (converted from count to amount) that are contained in the sample may or may not be known; the species of trees may be a pine or any other mixture of trees; the number of pinecones and needles may or may not be determined. In contrast to this potentially but not necessarily vague definition of entity X, the sample must be well defined in the sense of being separated from the rest of the world for measuring or counting, otherwise a quantity does not make sense. Therefore, the symbols nS(X) and mS(X) do not make logical sense and should be replaced by nX and mX.
Comment (5): The symbol M(X) is well defined to indicate the molar mass M(X) [g·mol-1] of entity X, but there remains a problem with an extension to obtain a consistent system of symbols for other derived quantities, when mass is normalized not only for amount [g·mol-1] but count [g·x-1] and volume [g·L-1] (or for the SI [kg·m-3]). In different contexts there are ad hoc practical symbols in use, but a formally consistent system of symbols does not exist, as shown in the following table, comparing canonical and practical symbols for harmonization.
- Table 1. Count, amount, volume, and mass normalized for count, amount, volume, and mass. The canonical symbols adhere to a consistent formal rule, and are compared with practical symbols that are commonly used. While it is not suggested to replace the practical by canonical symbols, the canonical symbols help to decode the meaning of the quantities expressed by these symbols by showing their isomorphic form. For example, compare the Avogadro constant NA with molar mass M(X) as canonical symbols NnX and MnX, or the count concentration CX with the inverse of the molar volume Vm(X)-1 as canonical symbols NVX and nVX, respectively.
Quantity Unit : Normalized for Unit = Canonical symbol Unit Practical symbol Quantity count NX x : count NX x = 1 1 -- -- amount nX mol : count NX x = nUX mol·x-1 NA-1 1/Avogadro constant volume VX m3 : count NX x = VUX m3·x-1 elementary volume mass mX kg : count NX x = MUX kg·x-1 elementary mass count NX x : amount nX mol = NnX x·mol-1 NA Avogadro constant amount nX mol : amount nX mol = 1 1 -- -- volume VX m3 : amount nX mol = VnX m3·mol-1 Vm(X) molar volume (IUPAC) mass mX kg : amount nX mol = MnX kg·mol-1 M(X) molar mass count NX x : volume VX m3 = NVX x·m-3 CX number concentration* (IUPAC) amount nX mol : volume VX m3 = nVX mol·m-3 Vm(X)-1 1/molar volume volume VX m3 : volume VX m3 = 1 1 -- -- mass mX kg : volume VX m3 = mVX kg·m-3 ρX density count NX x : mass mX kg = NmX x·kg-1 amount nX mol : mass mX kg = nmX mol·kg-1 M(X)-1 1/molar mass volume VX m3 : mass mX kg = VmX m3·kg-1 vX specific volume (IUPAC) mass mX kg : mass mX kg = 1 1 -- --
- * The term 'number concentration' is misleading and has to be replaced by 'count concentration' (see Number and count).
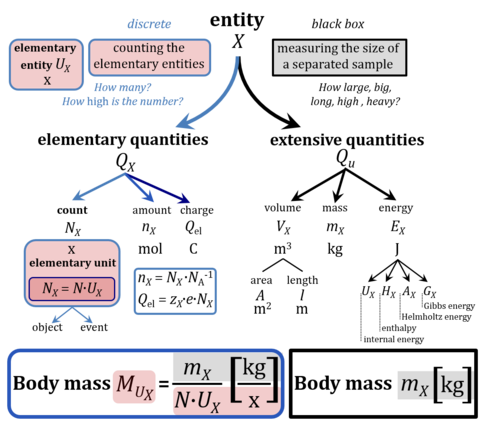
- The Figure compares elementary quantities that are stoichiometrically linked to counting of elementary entities (left) with extensive quantities based on measurements of a pure sample. Count, amount, and charge depend on the definition of elementary entities, whereas measurements of extensive quantities are independent of information on discrete entetic units. Red-shaded terms and units are not implemented in the SI. Entity X is used strictly in the sense of entity-type X. In practical language, however, the entity-type X = body in the context of human bodies is understood as indicating the elementary entity in terms of a single individual body, linked to the perception, that body mass is measured routinely on a sample of a single individual.
- Let a biomedical scientist measure the body mass of patients on the third floor. Here the meaning of X is definitely elementary, and body mass is "mass per body". Let the same biomedical scientist take blood samples from each patient, and move to the fourth floor for isolation of PBMC and platelets, taking a cell count, and measuring the cell mass. The meaning of X=body as perceived on the third floor (body mass MUX = 60 kg·x-1) switches subconsciously upon arrival in the fourth floor for studying respiration of living cells and X=ce, when cell mass is the mass measured in a sample containing a large number of cells (cell mass mX = 6 mg). All this works practically and automatically very well even in a single person, as long as the quantities obtained on the patient's blood cells (metabolic oxygen consumption per mass of cells) are not directly related to a quantity obtained on the individual patient (VO2max; respiratory capacity per individual, or VO2max/M per body mass).
Canonical recommendation
The BIPM and the Meter Convention (p. 118)
- The 59 SI member states and 42 states and economies that were associates of the General Conference should consider to extend the number of 10 Consultative Committees, which presently cover
- electricity and magnetism,
- photometry and radiometry,
- thermometry,
- length,
- time and frequency,
- ionizing radiation,
- units,
- mass and related quantities,
- amount of substance: metrology in chemistry and biology,
- acoustics, ultrasound and vibration.
- The 59 SI member states and 42 states and economies that were associates of the General Conference should consider to extend the number of 10 Consultative Committees, which presently cover
- Insufficient care is taken to emphasize the fundamental role of the quantity count. A consistent symbol for the quantity count needs to be defined. A unit and appropriate symbol for the unit of the quantity count needs to be implemented, such that a unit is not confused with a number, and a numeral is not used as a symbol for a unit. To take these deficiencies into account, it is recommended to implement an 11th Consultative Committee on:
- 11. elementary entities and count.